
Omni-MATH: A Universal Olympiad Level Mathematic Benchmark for Large Language Models

Introduction of Omni-MATH
Recent advancements in AI, particularly in large language models (LLMs), have led to significant breakthroughs in mathematical reasoning capabilities. However, existing benchmarks like GSM8K or MATH are now being solved with high accuracy (e.g., OpenAI o1 achieves 94.8% on MATH dataset), indicating their inadequacy for truly challenging these models. To mitigate this limitation, we propose a comprehensive and challenging benchmark specifically designed to assess LLMs' mathematical reasoning at the Olympiad level. Unlike existing Olympiad-related benchmarks, our dataset focuses exclusively on mathematics and comprises a vast collection of 4428 competition-level problems. These problems are meticulously categorized into 33 (and potentially more) sub-domains and span across 10 distinct difficulty levels, enabling a nuanced analysis of model performance across various mathematical disciplines and levels of complexity.
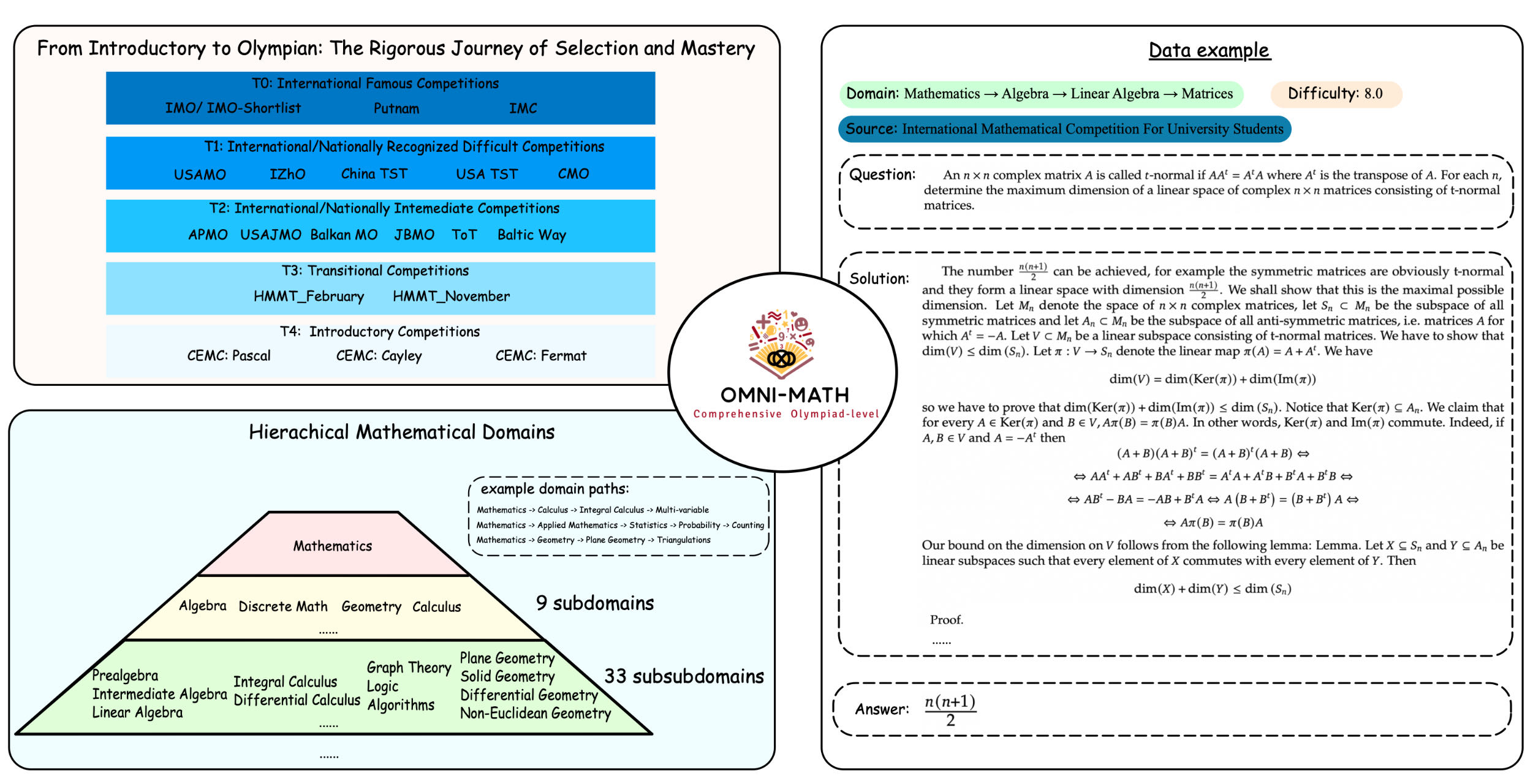
Difficulty: We conducted an extensive survey of mathematics competitions worldwide, categorizing them into five tiers based on their prominence, scale, and problem difficulty: Introductory, Transitional, Intermediate, National/International Difficult, and Famous Worldwide. To ensure accurate difficulty assessment, we rigorously adhered to the AoPS website's difficulty levels for problems listed there. For problems not on their list, we employed GPT-4o and few-shot prompting to give the difficulty tag.
Domain: We referenced established mathematics competition resources to construct a hierarchical classification tree for mathematical domains. Each problem within our dataset is assigned a specific domain classification path, reflecting the specific area of mathematics it tests.
Data Source: We collected problem statements and solutions from various international competitions and converted them into LaTeX format. For competitions lacking readily available solutions, we carefully selected problems from the AoPS website with high community recognition and reliable answers. All problems in our dataset include not only the final answer but also a detailed solution.
This newly proposed benchmark offers a valuable resource for researchers and developers to rigorously evaluate and further advance the mathematical reasoning abilities of LLMs.
| Publication Date | Overall Acc | Algebra | Precalculus | Calculus | Geometry | Discrete Mathematics | Number Theory | Applied Mathematics | Difficulty: 1-3 | Difficulty: 3-5 | Difficulty: 5-8 | Difficulty: 8-10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OpenAI o1-mini | 2024/9/13 | 60.54% | 67.82% | 68.18% | 60.94% | 51.50% | 37.68% | 61.74% | 60.52% | 82.23% | 63.10% | 49.11% | 42.69% |
| OpenAI o1-preview | 2024/9/13 | 52.55% | 57.70% | 57.47% | 53.91% | 43.11% | 31.26% | 49.67% | 53.42% | 80.11% | 50.83% | 42.25% | 37.71% |
| Qwen2.5-MATH-72b-Instruct | 2024/9/18 | 36.20% | 43.33% | 42.53% | 39.84% | 26.57% | 18.28% | 34.28% | 33.37% | 70.96% | 31.37% | 27.75% | 22.29% |
| Qwen2-MATH-72b-Instruct | 2024/8/8 | 33.68% | 40.27% | 37.50% | 27.34% | 22.53% | 17.50% | 30.01% | 32.96% | 70.10% | 29.06% | 24.71% | 17.98% |
| Qwen2.5-MATH-7b-Instruct | 2024/9/18 | 33.22% | 39.39% | 37.50% | 31.25% | 26.89% | 16.93% | 28.62% | 30.37% | 66.23% | 29.20% | 24.68% | 20.34% |
| GPT-4o | 2024/5/13 | 30.49% | 36.12% | 39.77% | 21.88% | 21.57% | 15.74% | 25.75% | 29.38% | 68.38% | 25.01% | 21.83% | 15.81% |
| Qwen2-MATH-7b-Instruct | 2024/8/8 | 29.36% | 36.08% | 35.23% | 24.22% | 18.68% | 14.41% | 27.04% | 25.93% | 63.52% | 24.30% | 21.52% | 18.54% |
| NuminaMATH-72B-COT | 2024/7/19 | 28.45% | 34.74% | 27.27% | 21.88% | 20.41% | 16.95% | 23.47% | 25.06% | 65.63% | 23.70% | 20.33% | 21.08% |
| Claude-3.5-SONNET | 2024/6/21 | 26.23% | 30.30% | 29.55% | 19.53% | 17.70% | 15.74% | 19.51% | 26.70% | 66.23% | 18.91% | 18.27% | 17.41% |
| DeepSeek-Coder-V2 | 2024/6/17 | 25.78% | 30.24% | 35.23% | 15.62% | 17.99% | 12.71% | 20.90% | 23.58% | 65.38% | 18.84% | 18.06% | 14.61% |
| MetaLlama-3.1-70B-instruct | 2024/8/2 | 24.16% | 29.15% | 16.05% | 18.75% | 14.76% | 11.74% | 17.03% | 24.66% | 62.66% | 16.82% | 16.95% | 13.71% |
| DeepSeek-Coder-V2-Lite-Instruct | 2024/6/17 | 19.73% | 24.55% | 23.86% | 13.28% | 13.06% | 8.92% | 15.88% | 16.81% | 55.93% | 13.15% | 12.86% | 9.55% |
| Mathstral-7B-v0.1 | 2024/7/16 | 19.13% | 23.99% | 25.00% | 13.28% | 12.19% | 10.04% | 14.58% | 16.30% | 53.07% | 10.93% | 15.29% | 11.86% |
| DeepSeekMATH-7b-RL | 2024/2/6 | 16.12% | 21.28% | 20.45% | 12.50% | 9.87% | 7.71% | 9.98% | 13.58% | 49.07% | 9.11% | 11.49% | 7.80% |
| InternLM2-math-plus-mixtral8*22B | 2024/5/24 | 14.24% | 18.19% | 12.50% | 10.16% | 8.70% | 8.03% | 10.09% | 12.36% | 42.78% | 8.01% | 10.35% | 6.74% |
Rule-based Evaluation Results
| Model | Rule-based Accuracy |
|---|---|
| o1-mini | 62.2% |
| o1-preview | 51.7% |
| Qwen-QwQ | 49.6% |
| qwen2.5-MATH-72b-Instruct | 36.2% |
| qwen2.5-MATH-7b-Instruct | 32.3% |
| GPT-4o | 29.2% |
| NuminaMATH-72b-cot | 26.2% |
| DeepseekMATH-7b-RL | 14.9% |
To make our benchmark more user-friendly (eliminating the need for an additional model-based evaluator), we extracted the subset of Omni-MATH problems suitable for rule-based evaluation and made some modifications to the evaluation code of Qwen2.5-MATH. This allows for easier model evaluation. To validate our rule-based evaluation, we conducted evaluations on models using the adapted repository. The evaluation results are as follows and are generally consistent with the results on the Omni-MATH leaderboard(GPT-4o Evaluation).
Data Explorer
| Domain | |
| Difficulty | |
| Problem Source | |
| Question | |
| Solution | |
| Answer |